Here, we show a simple example of a salmon operating model where all fish mature at age 3 and follows the structure of an analysis done in AHA. The historical spool-up is not informed by an estimation model. The model is used to project the proposed management levers to determine the equilibrium properties of the system.
We create several S4 objects, the Bio object contains
the natural biological dynamics, including the maturity ogive
p_mature, fecundity, as well as the density-dependent
survival of smolts through the capacity and productivity parameters
(capacity_smolt and kappa, respectively).
The first example will be deterministic. With salmonMSE, we must run at minimum 2 simulation replicates, but we will run 3 simulations where the biological parameters, as well as the results, are identical among simulations.
To accommodate the life stage within the age structured model, we
model ocean survival as an equivalent instantaneous rate
Mjuv_NOS where all mortality occurs in the age class prior
to maturation, i.e., age 2.
library(salmonMSE)
class?SOM # Definition of inputs
SAR <- 0.01 # Marine survival
nsim <- 3 # Number of simulations
Bio <- new(
"Bio",
maxage = 3,
p_mature = c(0, 0, 1),
SRrel = "BH",
capacity_smolt = 17250, # Beverton-Holt asymptote. Not unfished capacity!
kappa = 3, # Productivity in recruits per spawner
Mjuv_NOS = c(0, -log(SAR), 0), # Convert marine survival to an instantaneous mortality rate
fec = c(0, 0, 5040), # Spawning fecundity of NOS and HOS
p_female = 0.49,
s_enroute = 1
)The next three objects control the management of the conservation unit through habitat, hatchery, and harvest options.
Let’s leave the habitat unchanged from the Bio
object:
Habitat <- new(
"Habitat",
capacity_smolt_improve = 1, # Keep carrying capacity unchanged
kappa_improve = 1 # Keep productivity unchanged
)Next, we work on the hatchery dynamics.
Below, we have a management target to release 10,000 yearlings
annually. In comparison, the carrying capacity of the natural
environment is 17,250 smolts. Users also specify the survival of
broodtake (s_prespawn), eggs in the hatchery
(s_egg_smolt and s_egg_subyearling), the
target proportion of natural spawners in the broodtake
(ptarget_NOB), and the maximum proportion of natural
spawners to be used as broodtake (pmax_NOB). The target
proportion can be obtained when the mark rate m = 1 and
broodstock origin can be identified.
We place some additional constraints are placed which may prevent us
from realizing the target releases. In each time step of the projection,
the model calculates the required number of eggs annually for the target
releases. The natural broodtake (NOB) and hatchery broodtake (HOB) are
removed from the escapement to reach the target egg production and
maintain NOB/(NOB + HOB) = ptarget_NOB. The proportion of
NOB to the natural origin escapement cannot exceed
pmax_NOB. If the target egg production cannot be reached,
then the NOB is taken in accordance with pmax_NOB and HOB
is taken (up to the total hatchery origin escapement returned to the
hatchery) to meet the target egg production.
We also need to specify the relative spawning success of HOS, and various parameters that control fitness of hatchery fish in the natural environment.
Hatchery <- new(
"Hatchery",
n_yearling = 10000, # Management lever. No hatchery if both this line and next line are zero
n_subyearling = 0, # Management lever. No hatchery if both this line and previous line are zero
s_prespawn = 1, # Survival prior to spawning
s_egg_smolt = 0.92, # Survival of eggs in hatchery
s_egg_subyearling = 1,
Mjuv_HOS = Bio@Mjuv_NOS,
gamma = 0.8,
m = 1, # Mark rate of hatchery releases
pmax_esc = 1, # Maximum proportion of escapement (after en route mortality) that could be used as broodtake
pmax_NOB = 0.7,
ptarget_NOB = 0.51,
phatchery = 0.8,
premove_HOS = 0,
theta = c(100, 80),
rel_loss = c(0.5, 0.4, 0.1),
fec_brood = c(0, 0, 5040),
fitness_type = c("Ford", "none"),
zbar_start = c(93.1, 92),
fitness_variance = 10,
selection_strength = 3,
heritability = 0.5,
fitness_floor = 0.5
)We specify a harvest rate of 0.203 for the terminal fishery (mature component). No hatchery fish are marked.
Harvest <- new(
"Harvest",
u_preterminal = 0, # No pre-terminal fishery
u_terminal = 0.203, # Specify fixed harvest rate of mature fish
MSF = FALSE, # No mark-selective fishing
release_mort = c(0.1, 0.1),
vulPT = c(0, 0, 0),
vulT = c(1, 1, 1)
)To start the projection, we specify the conditions for the spool-up
with the Historical object. We will have a two-year spool-up with an
escapement of 1000 natural origin fish and 1000 hatchery origin fish
each in the first generation (for all simulations). This is accomplished
by setting a spool-up period of 2 years (nyears) and
specify the immature abundance of age 1 fish at the beginning of year 1
and age 2 fish at the start of year 2. Since we model ocean survival
during age 2, abundance of the cohort doesn’t change.
# Return of 1000 natural and hatchery fish each for the first generation
nyears <- 2
HistN <- array(0, c(nsim, Bio@maxage, nyears+1, 2))
HistN[, 1, 1, ] <- HistN[, 2, 2, ] <- 1000/SAR
Historical <- new(
"Historical",
HistN = HistN
)Now let’s stitch together the operating model and run the simulation
for 50 projection years (proyears).
SOM <- new(
"SOM",
Bio, Habitat, Hatchery, Harvest, Historical,
nsim = nsim, nyears = 2, proyears = 50
)
SMSE <- salmonMSE(SOM)With a simple salmon model, we can run AHA and compare the trajectory of the population. As we can see, the number of NOS in both models is slowly equilibriating to approximately 70.
SAHA <- AHA(SOM, ngen = 20)
# Compare NOS
SAHA$NOS
SMSE@NOS[, 1, ]
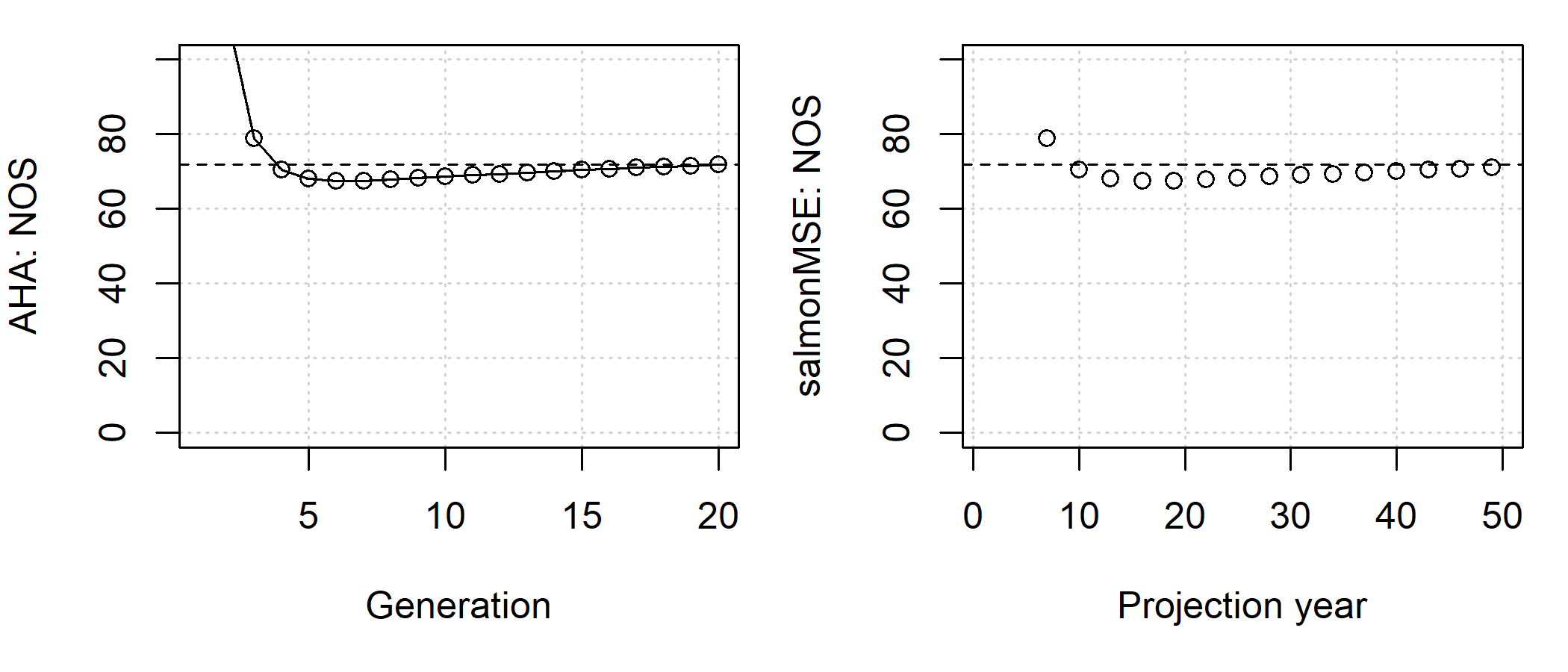
Comparison of the abundance of NOS between AHA (by generation) and salmonMSE (by year) given identical biological parameters, hatchery releases, and terminal fishery harvest rate in the simple example.
Stochastic simulations
Let’s repeat the simple example with stochasticity on the productivity parameter (“kappa”, units of recruits/spawner). To do this, we sample productivity from a distribution and we run 100 simulations. This incorporates our uncertainty in understanding of natural productivity in the evaluation of the management strategy.
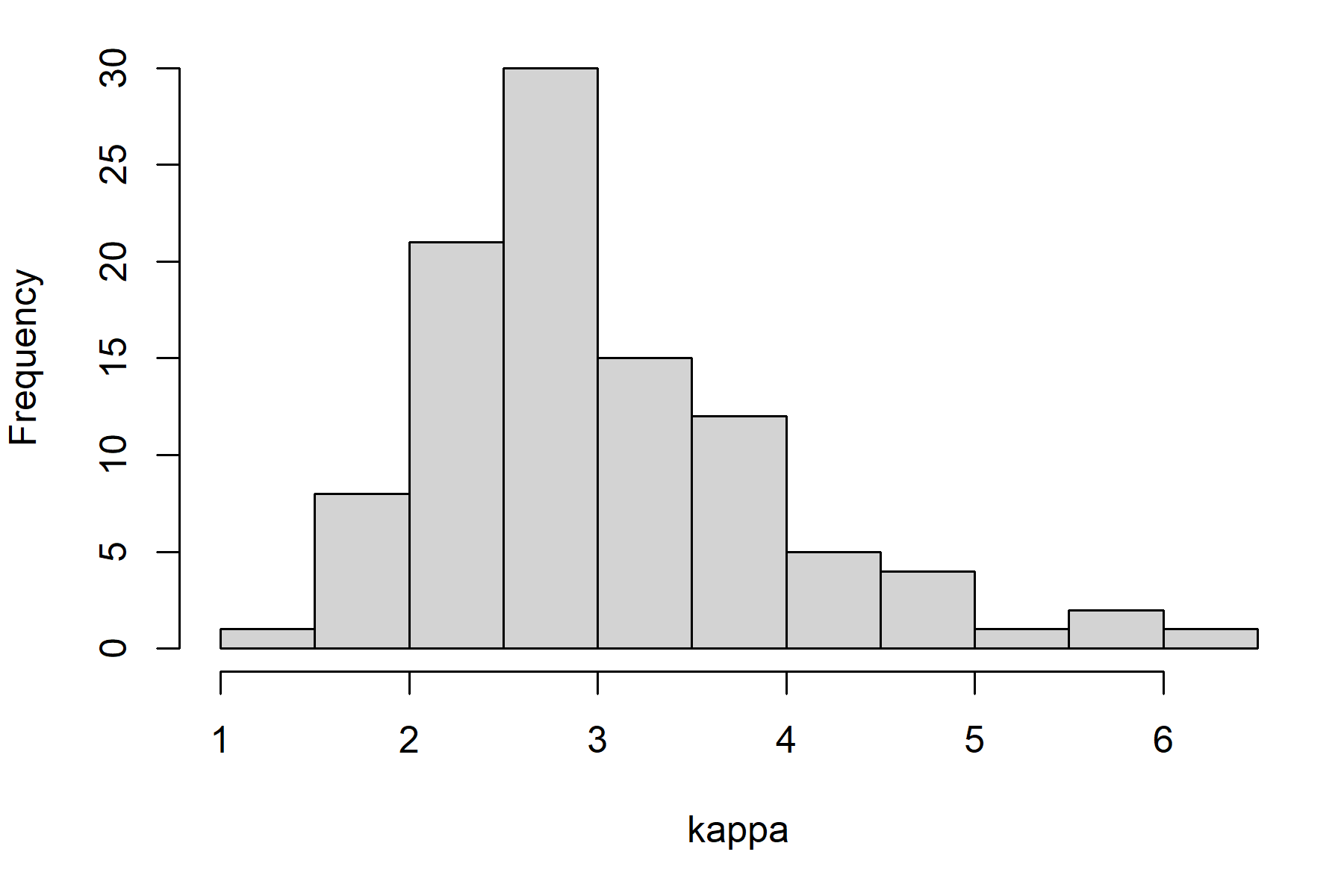
Histogram of the productivity (kappa) values sampled for our stochastic operating model.
SAR <- 0.01
nsim_stochastic <- 100
# Sample productivity
set.seed(100)
kappa_mean <- 3
kappa_sd <- 0.3
kappa <- rlnorm(nsim_stochastic, log(kappa_mean) - 0.5 * kappa_sd^2, kappa_sd)
Bio_stochastic <- new(
"Bio",
maxage = 3,
p_mature = c(0, 0, 1),
SRrel = "BH",
capacity_smolt = 17250,
kappa = kappa,
Mjuv_NOS = c(0, -log(SAR), 0),
fec = c(0, 0, 5040),
p_female = 0.49,
s_enroute = 1
)
nyears <- 2
HistN <- array(0, c(nsim_stochastic, Bio_stochastic@maxage, nyears+1, 2))
HistN[, 1, 1, ] <- HistN[, 2, 2, ] <- 1000/SAR
Historical <- new(
"Historical",
HistN = HistN
)
SOM_stochastic <- new(
"SOM",
Bio_stochastic, Habitat, Hatchery, Harvest, Historical,
nsim = nsim_stochastic, nyears = 2, proyears = 50
)
SMSE_stochastic <- salmonMSE(SOM_stochastic)We expect a distribution in the state variables during the projection. Let’s take a look at PNI, where we can plot the median and 95 percent range in values annually from the projection:
plot_statevar_ts(SMSE_stochastic, "PNI", quant = TRUE)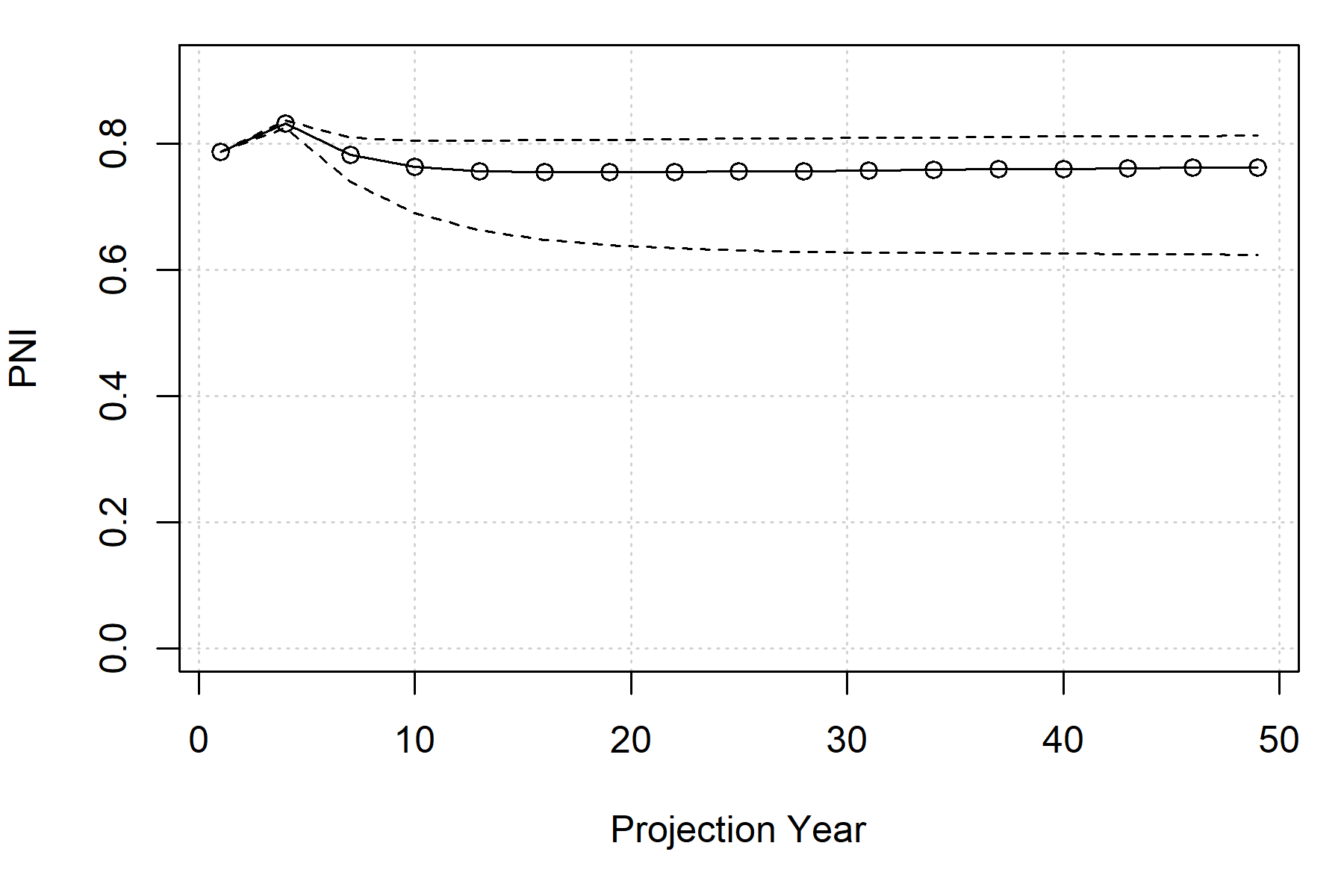
Here is the distribution of PNI in the last projection year:
plot_statevar_hist(SMSE_stochastic, "PNI", y = 49)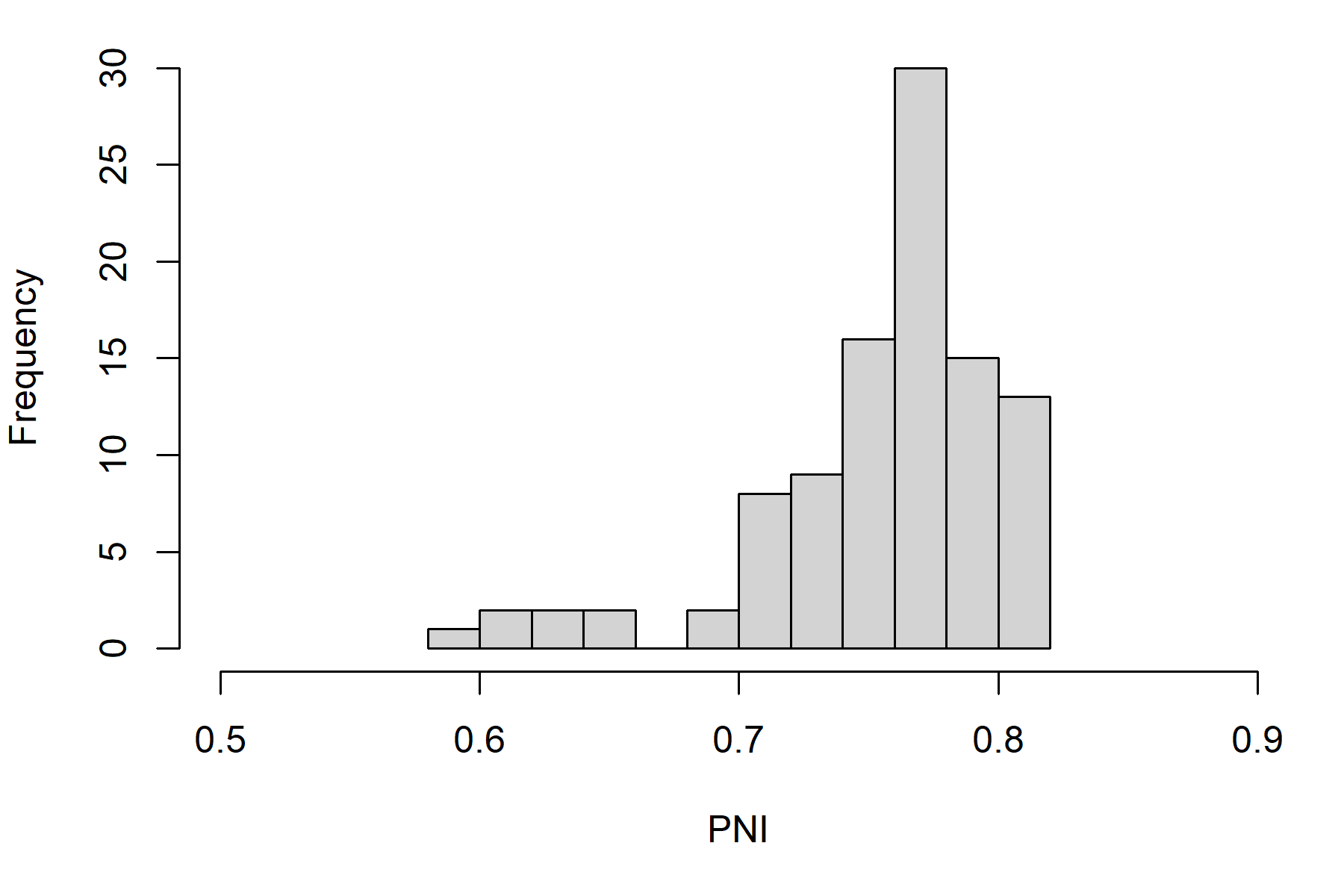
From such models, we can develop performance metrics that make probabilistic statements about the system dynamics for each set of management actions. For example, we calculate the long-term probability that PNI is at least 0.80:
PNI_LT <- SMSE_stochastic@PNI[, 1, 49]
mean(PNI_LT >= 0.5)#> [1] 0.13The quantiles can also be calculated for our performance metric from the stochastic replicates:
#> 2.5% 50% 97.5%
#> 0.6266439 0.7634803 0.8133749Here is the relationship between the performance metrics and productivity:
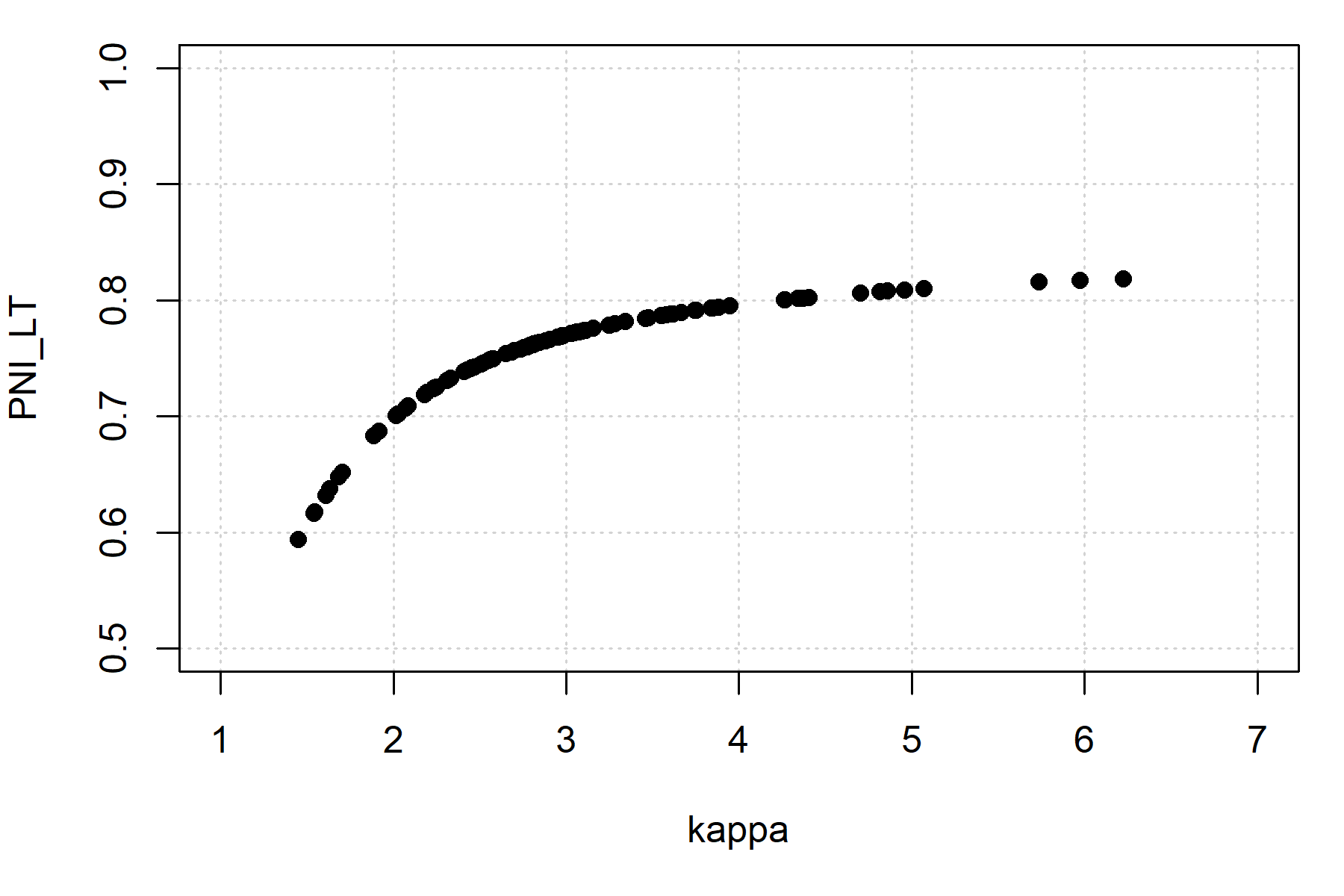
A summary Markdown report can be generated with the
report() function:
report(SMSE_stochastic)